Explorando las Relaciones Métricas en Triángulos: Un Enfoque Práctico
Las relaciones métricas en triángulos son un aspecto fundamental de la geometría que nos permite comprender y calcular diversas medidas relacionadas con los lados, ángulos y alturas de un triángulo. En este artículo, nos sumergiremos en este concepto clave, proporcionando una visión clara y ejemplos prácticos para su comprensión.
Entendiendo las Relaciones Métricas
Las relaciones métricas se basan en el teorema de Tales y en las propiedades de las proporciones. Este teorema establece que si trazamos una línea paralela a uno de los lados de un triángulo, los segmentos resultantes en los otros dos lados son proporcionales a los segmentos originales. Esta propiedad es la base de muchas relaciones métricas en triángulos.
Explorando las Relaciones Métricas en Triángulos: Un Enfoque Práctico
Las relaciones métricas en triángulos son un aspecto fundamental de la geometría que nos permite comprender y calcular diversas medidas relacionadas con los lados, ángulos y alturas de un triángulo. En este artículo, nos sumergiremos en este concepto clave, proporcionando una visión clara y ejemplos prácticos para su comprensión.
Entendiendo las Relaciones Métricas
Las relaciones métricas se basan en el teorema de Tales y en las propiedades de las proporciones. Este teorema establece que si trazamos una línea paralela a uno de los lados de un triángulo, los segmentos resultantes en los otros dos lados son proporcionales a los segmentos originales. Esta propiedad es la base de muchas relaciones métricas en triángulos.
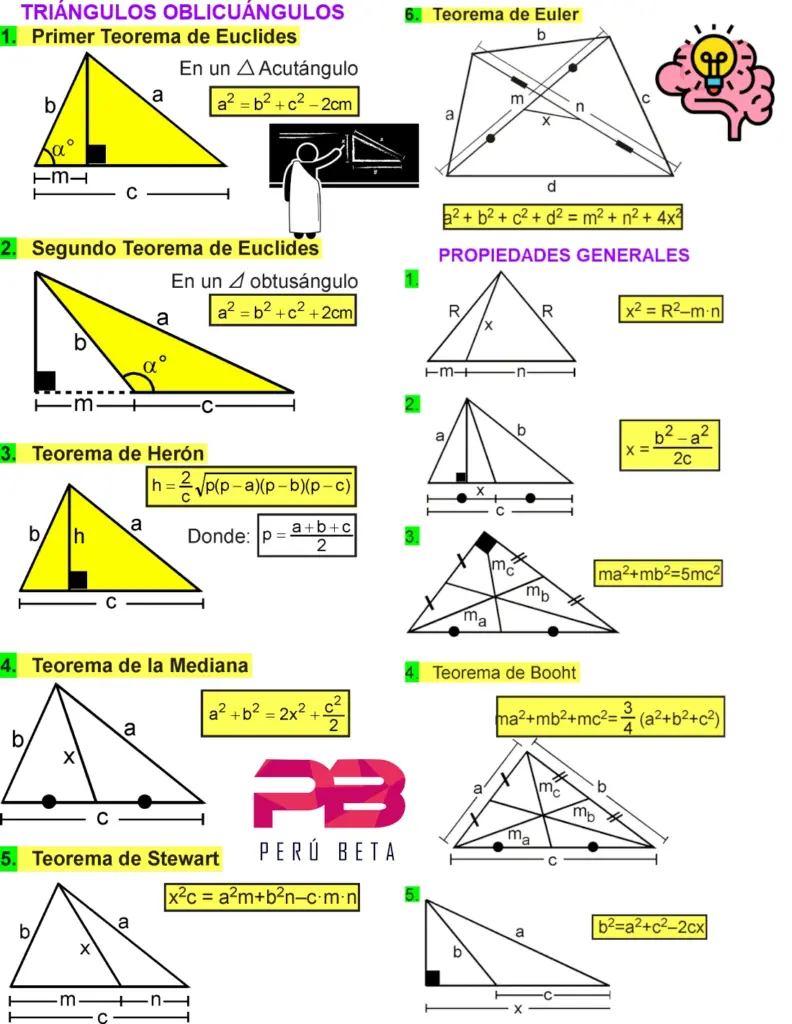
Ejemplos Prácticos de Relaciones Métricas
- La Longitud de la Mediana:Una mediana de un triángulo es una línea que conecta un vértice con el punto medio del lado opuesto. La longitud de una mediana es igual a la mitad de la longitud del lado opuesto. Por ejemplo, si un triángulo tiene un lado de longitud 6 cm y la mediana desde el vértice opuesto mide 4 cm, entonces el lado opuesto tendría una longitud de 8 cm (doble de la longitud de la mediana).
- La Altura de un Triángulo:La altura de un triángulo es la distancia perpendicular desde un vértice hasta el lado opuesto. Según el teorema de Tales, si trazamos una altura desde un vértice al lado opuesto, los segmentos resultantes son proporcionales a los segmentos del lado opuesto y la hipotenusa del triángulo. Esta relación es útil para calcular alturas y áreas de triángulos.

Aplicaciones en la Vida Real | Relaciones Métricas
Las relaciones métricas en triángulos tienen numerosas aplicaciones en la vida cotidiana y en diversas disciplinas, como la arquitectura, la ingeniería y la cartografía. Por ejemplo, los ingenieros utilizan estas relaciones para calcular la altura de estructuras, mientras que los arquitectos las emplean para diseñar y construir edificios de manera precisa.






